Índice
Número índice
Un número índice es una medida estadística que permite estudiar las fluctuaciones o variaciones de una magnitud o de más de una en relación al tiempo o al espacio. Los índices más habituales son los que realizan las comparaciones en el tiempo, por lo que, como veremos más adelante, los números índices son en realidad series temporales.
[editar]
Aproximación
Los números índices nacen de la necesidad de conocer en profundidad la magnitud de un fenómeno y poder realizar comparaciones del mismo en distintos territorios o a lo largo del tiempo. Una forma inicial de resolver el problema es referir cada situación a la anterior, pero esto no hace viable la posibilidad de comparaciones significativas, al menos directamente, salvo en lo concerniente a dos de ellas inmediatas. Por esto es más conveniente escoger una situación determinada como punto de referencia inicial, para remitir a ella todas las demás observaciones, esta situación se denomina situación base y las comparaciones que se realizan vienen establecidas a través de un número índice. Los números índices, o simplemente índices, proporcionan comparaciones entre datos correspondientes a diferentes situaciones, escalonadas con arreglo a algún criterio conocido (por ejemplo, por el transcurso del tiempo).
Si definimos a 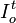 como el Número Índice de un determinado valor o bien en el período t, respecto al período base o, entonces
como el Número Índice de un determinado valor o bien en el período t, respecto al período base o, entonces
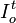 como el Número Índice de un determinado valor o bien en el período t, respecto al período base o, entonces
como el Número Índice de un determinado valor o bien en el período t, respecto al período base o, entonces
donde  representa el valor del bien en el período t y
representa el valor del bien en el período t y  el valor del bien en el periodo o.
el valor del bien en el periodo o.
 representa el valor del bien en el período t y
representa el valor del bien en el período t y  el valor del bien en el periodo o.
el valor del bien en el periodo o.
Las comparaciones, en estadística, entre distintas variables o entre los valores de una sola variable pueden realizarse de distintas formas. Las formas más simples son las que se llevan a cabo por diferencia o aquellas que se realizan por cociente. Estas últimas tienen la ventaja frente a las primeras que eliminan el problema de las unidades de medida. En cambio el segundo de los procedimientos, aunque no adolece de ese problema, puede plantear problemas relativos a elegir la unidad de referencia para realizar las comparaciones.
[editar]
Propiedades
Uno de los problemas de mayor importancia a la hora de elaborar un número índice es el conseguir que éste sea adecuadamente representativo, para ello es preciso que el índice cumpla ciertas propiedades de carácter matemático y reúna ciertos requisitos en su definición:
- Identidad. Cuando el período base y el de comparación coinciden, el índice debe ser igual a uno.
- Inversión. Si en un índice se invierten los períodos base y de comparación, el índice toma el valor recíproco al anterior.
- Circular. Si se multiplica el índice de un período Z con relación a un período Y por el índice de Y con relación a X, el producto ha de ser el índice de Z con relación a X.
- Existencia. El índice ha de tomar valores reales y finitos para cualquier valor de la variable observada.
- Proporcionalidad. El índice elaborado sobre unos determinados valores de una variable ha de ser proporcional al índice correspondiente a los valores de esa variable multiplicados por un mismo número K.
- Variación proporcional. Si los valores de la variable varían en una cierta cuantía, el índice varía proporcionalmente.
- Inalterabilidad. Si se introduce una nueva modalidad en el índice complejo, de tal manera que el valor de éste coincide con el del índice simple de aquella, el índice complejo no varía.
- Homogeneidad. El valor de un índice no ha de ser afectado por modificaciones de las unidades de medida.
[editar]
Índices simples y complejos
Cuando se realiza una comparación entre los valores de una sola magnitud se obtienen índices simples, En cambio, si se trabaja con más de una magnitud a la vez, se habla de índices complejos. En los dos casos se comparan siempre dos situaciones, una de las cuales se considera como referencia. Cuando se trata de comparaciones temporales, a la situación inicial, se le conoce como periodo base o referencia, mientras que el periodo objeto de comparación se denomina corriente o actual. Para elaborar un número índice de carácter simple, se asigna al periodo que es objeto de referencia el valor 100, de esta manera los números índices de las distintas observaciones posteriores, no son otra cosa que porcentajes de cada valor con respecto al de la referencia. Dentro de los índices complejos se distingue entre índices ponderados y no ponderados, según el peso que se le de a los distintos valores.



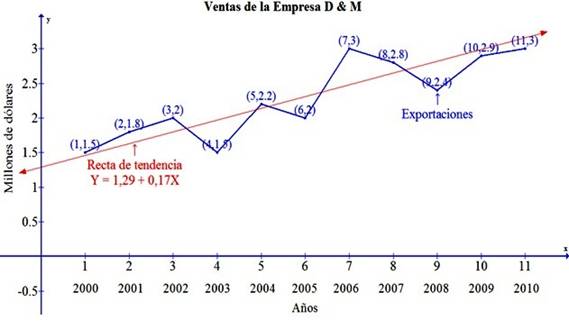
 al ser positiva indica que existe una tendencia ascendente de las
al ser positiva indica que existe una tendencia ascendente de las  indica el punto en donde la recta interseca al eje Y cuando X = 0, es decir indica las exportaciones estimadas para el año 1996 igual a 3,22.
indica el punto en donde la recta interseca al eje Y cuando X = 0, es decir indica las exportaciones estimadas para el año 1996 igual a 3,22.


 y
y 

 y
y  los cuales se reemplazan en la ecuación de la recta de tendencia, la cual es:
los cuales se reemplazan en la ecuación de la recta de tendencia, la cual es:




 es positiva, la recta tiene una tendencia ascendente (pendiente positiva).
es positiva, la recta tiene una tendencia ascendente (pendiente positiva).



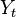 : variable dependiente, explicada o regresando.
: variable dependiente, explicada o regresando. : variables explicativas, independientes o regresores.
: variables explicativas, independientes o regresores.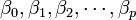 : parámetros, miden la influencia que las variables explicativas tienen sobre el regresando.
: parámetros, miden la influencia que las variables explicativas tienen sobre el regresando. es la intersección o término "constante", las
es la intersección o término "constante", las  son los parámetros respectivos a cada variable independiente, y
son los parámetros respectivos a cada variable independiente, y  es el número de parámetros independientes a tener en cuenta en la regresión. La regresión lineal puede ser contrastada con la regresión no lineal.
es el número de parámetros independientes a tener en cuenta en la regresión. La regresión lineal puede ser contrastada con la regresión no lineal.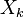 (k = 1,...K), o cualquier transformación de éstas, que generan un hiperplano de parámetros
(k = 1,...K), o cualquier transformación de éstas, que generan un hiperplano de parámetros  desconocidos:
desconocidos:
 es la perturbación aleatoria que recoge todos aquellos factores de la realidad no controlables u observables y que por tanto se asocian con el azar, y es la que confiere al modelo su carácter estocástico. En el caso más sencillo, con una sola variable explicativa, el hiperplano es una recta:
es la perturbación aleatoria que recoge todos aquellos factores de la realidad no controlables u observables y que por tanto se asocian con el azar, y es la que confiere al modelo su carácter estocástico. En el caso más sencillo, con una sola variable explicativa, el hiperplano es una recta:

 , son los coeficientes de regresión, sin que se pueda garantizar que coinciden con parámetros reales del proceso generador. Por tanto, en
, son los coeficientes de regresión, sin que se pueda garantizar que coinciden con parámetros reales del proceso generador. Por tanto, en
 son por su parte estimaciones de la perturbación aleatoria o errores.
son por su parte estimaciones de la perturbación aleatoria o errores.
 para todo t
para todo t en torno a su valor esperado es siempre la misma.
en torno a su valor esperado es siempre la misma. para todo t,s con t distinto de s
para todo t,s con t distinto de s Suponemos que no existen errores de especificación en el modelo ni errores de medida en las variables explicativas
Suponemos que no existen errores de especificación en el modelo ni errores de medida en las variables explicativas

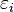 es el error asociado a la medición del valor
es el error asociado a la medición del valor  y siguen los supuestos de modo que
y siguen los supuestos de modo que  (media cero, varianza constante e igual a un
(media cero, varianza constante e igual a un  y
y  con
con  ).
).
 y
y 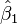 e igualando a cero, se obtiene:
e igualando a cero, se obtiene:
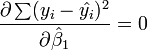


 es que un incremento en Xi de una unidad, Yi incrementará en
es que un incremento en Xi de una unidad, Yi incrementará en 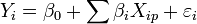
 del valor
del valor  y siguen los supuestos de modo que
y siguen los supuestos de modo que 
